Insights into Toronto’s Foodservice Market

Comments

wordcloud

Podcast

Give your eyes a break—listen to my article instead!

Abstract

The project delivers valuable decision driven insights into Toronto's foodservice industry by employing modern-day data science tools. K means, an unsupervised clustering algorithm is applied to segregate the city's restaurant market into clusters based on the types of restaurants established in the city. Relationship between foodservice market of a neighbourhood and its location relative to the city centre along with relationships within various types of restaurants are analysed using inferential statistics.

Introduction/Business Understanding

Background

By 2022, quick-service restaurants are expected to remain the largest segment in the foodservice industry in Canada followed by full-service restaurants. However, Toronto’s landscape is unique compared to the rest of the country. Toronto has comparatively higher percentages of coffee shops and fine dining restaurants compared to the national average. There are also more restaurants serving European menus in Toronto than in other places, whereas the “hamburger” type menus are relatively scarce in the city. It is interesting to note that Toronto has a very strong presence of independently owned restaurants making up more than 90% of the city’s foodservice market.

Area of Interest

With a blooming foodservice market, Toronto constantly attracts new restaurants and eateries. The target audience of the project are the investors and potential restaurant owners are often faced with several market research questions such as the current market landscape in the area of interest, the type of restaurant that fits well with the neighbourhood, the best location for a particular type of restaurant, etc. However, since Toronto's foodservice market is unique to itself, new owners cannot simply rely on a nationwide analysis. A city-specific analysis is what would benefit anyone who intends to start a new restaurant in Toronto and that is precisely what this project presents.

Problem Statement

This project aims to provide valuable insights into Toronto’s current foodservice market such as distribution of restaurant types by locations, variations in density of restaurants and suggestive analysis of types of restaurants to benefit new and potential restaurant owners and investors.

Analytical Approach

Clustering

The approach is to categorize types of restaurants in Toronto into various clusters and map them to their geographical locations. A visualization map of Toronto would illustrate these clusters cast across its postal codes.

Correlation

Further analysis is done to identify any correlation between restaurants in the neighbourhood and its distance from the city centre, and any significant correlations within types of restaurants.

Data Acquisition

Data requirements

The data required for the project includes the list of postal codes of the city, types of restaurants in each location, number of restaurants of each type, distances of restaurants from the city centre, and the geographical coordinates of the postal codes to visualize the data in a map.

Data collection

Neighbourhood data

Postal code data for Toronto is scraped from the following Wikipedia page:

Source: https://en.wikipedia.org/wiki/List_of_postal_codes_of_Canada:_M

Data points:

  • Postal code

  • Borough

  • Neighbourhood

Geographical coordinates

Geographical coordinates data is extracted using Mapquest’s Geocoding API:

Source: https://developer.mapquest.com/documentation/geocoding-api/

Alternate source (Google API): https://link.datascience.eu.org/p001d1

Data points:

  • Postal code

  • Latitude

  • Longitude

Foodservice market data

Restaurant data is extracted from FourSquare’s Places API. FourSquare data is classified into various categories and sub-categories. Categories are identified by the tag "Category ID". The category of interest here is Food and the category ID for food is 4d4b7105d754a06374d81259. The sub-categories of the food category are various types of restaurants located in the venue.

Source: https://developer.foursquare.com/docs/api/endpoints

Data points:

  • Postal code

  • Venue Latitude

  • Venue Longitude

  • Venue category

  • Venue subcategory

Table 1. Data points and data sources.

Datapoint Source
Postal Code Wikipedia
Borough Wikipedia
Neighbourhood Wikipedia
Postal Code MapQuest Geocoding API
Latitude MapQuest Geocoding API
Longitude MapQuest Geocoding API
Postal Code FourSquare Places API
Venue Latitude FourSquare Places API
Venue Longitude FourSquare Places API
Venue Category FourSquare Places API
Venue Subcategory FourSquare Places API

Code for data collection

Importing libraries

In [1]:
import numpy as np  # Numpy library
import pandas as pd  # library for data analysis
import json  # library to handle JSON files
import geocoder  # convert an address into latitude and longitude values
from geopy.geocoders import Nominatim  # convert an address into latitude and longitude values
import requests  # library to handle requests
import matplotlib.cm as cm  # Matplotlib and associated plotting modules
import matplotlib.colors as colors
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans  # import k-means from clustering stage
import folium  # map rendering library
import seaborn as sns  # Seaborn
from scipy.stats import pearsonr  # Pearson correlation library
from getpass import getpass as gp  # to hide API keys from being displayed
from tabulate import tabulate  # to pretty print tabular data
In [2]:
pd.set_option('display.max_columns', 10)
pd.set_option('display.max_rows', 10)

Scraping neighbourhood data from the web

Since the neighbourhood and postal code data is already in the form of a table, we can use the pandas read_html which looks for tabular data and loads it into a data frame

In [2]:
df_PostalCodes = \
    pd.read_html('https://en.wikipedia.org/wiki/List_of_postal_codes_of_Canada:_M'
                 )[0]

Collecting geographical coordinates from MapQuest

Documentation for MapQuest Geocoding API is available at https://geocoder.readthedocs.io/providers/MapQuest.html

In [4]:
MapQuest_key = gp("Enter your MapQuest API key")
In [39]:
# Collecting coordinates from MapQuest geocode API for a sample of 5 postal codes.

sample = 5
df_MQ_Coordinates = pd.DataFrame(columns=['Latitude', 'Longitude'])
for i in range(sample):
    g = geocoder.mapquest(df_PostalCodes.loc[i, 'Postcode']
                          + ', Toronto, Ontario', key=MapQuest_key)
    df_MQ_Coordinates.loc[i] = g.latlng

Extracting types of restaurants from FourSquare

FourSquare's category ID for Food is 4d4b7105d754a06374d81259. Venues will be searched in each neighbourhood by this category ID. The restaurant type, which is the sub-category, of each venue is extracted. If there are no restaurants in a neighbourhood, then the restaurant type will be assigned as "No Restaurants".

In [34]:
FourSquare_client_ID = gp('Enter your FourSquare Client ID')
FourSquare_client_secret = gp('Enter your FourSquare Client Secret')
FourSquare_API_version = '20190801'  # Foursquare API version
In [40]:
# Extracting restaurant data for a sample of 5 locations

df_MQ_Location = pd.concat([df_PostalCodes.head(sample),
                           df_MQ_Coordinates], axis=1)
df_RestaurantTypes = pd.DataFrame(columns=['RestaurantType',
                                  'PostalCode'])
for (index, row) in df_MQ_Location.iterrows():
    limit = 100  # limit of number of venues returned by Foursquare API
    radius = 300  # define radius
    cat_id = '4d4b7105d754a06374d81259'  # Category: Food
    url = 'https://api.foursquare.com/v2/venues/search?&client_id={}&client_secret={}&v={}&ll={},{}&radius={}&limit={}&categoryId={}'.format(
        FourSquare_client_ID,
        FourSquare_client_secret,
        FourSquare_API_version,
        row['Latitude'],
        row['Longitude'],
        radius,
        limit,
        cat_id,
        )
    df_results = pd.DataFrame(list(venue['categories'][0]['name']
                              for venue in
                              requests.get(url).json()['response']['venues']), columns=['RestaurantType'])
    if df_results.shape[0] == 0:
        df_results.loc[0, ['RestaurantType']] = 'No Restaurants'
    df_results['PostalCode'] = row['Postcode']
    df_RestaurantTypes = pd.concat([df_RestaurantTypes, df_results])
df_RestaurantTypes.reset_index(drop=True, inplace=True)

Data Preparation and Feature Extraction

Data understanding

In [41]:
# Checking neighbourhood data

print('Shape:', df_PostalCodes.shape)
df_PostalCodes.head()

Shape: (288, 3)
Out[41]:
Postcode Borough Neighbourhood
0 M1A Not assigned Not assigned
1 M2A Not assigned Not assigned
2 M3A North York Parkwoods
3 M4A North York Victoria Village
4 M5A Downtown Toronto Harbourfront

The neighbourhood data contains the variables Postcode, Borough and Neighbourhood.

In [42]:
# Checking geographical coordinates data

print('Shape:', df_MQ_Coordinates.shape)
df_MQ_Coordinates.head()

Shape: (5, 2)
Out[42]:
Latitude Longitude
0 43.63175 -79.41944
1 43.63175 -79.41944
2 43.76523 -79.33701
3 43.73279 -79.31051
4 43.65331 -79.36646

The geographical data from MapQuest contains variables PostalCode, Latitude and Longitude.

In [43]:
df_RestaurantTypes.head()
Out[43]:
RestaurantType PostalCode
0 Food Truck M1A
1 Poutine Place M1A
2 Fast Food Restaurant M1A
3 Wings Joint M1A
4 Donut Shop M1A

The FourSquare API data contains records of variables RestaurantType and PostalCode.

Data Preperation

Postal code and neighbourhood data

In [3]:
# Renaming column names

df_PostalCodes.rename(columns={'Postcode': 'PostalCode'}, inplace=True)

# Ignore cells with a borough that is 'Not assigned'

df_PostalCodes = df_PostalCodes.query("Borough != 'Not assigned'"
        ).reset_index(drop=True)

# Combining neighbourhoods belonging to same postal code

df_PostalCodes = df_PostalCodes.groupby('PostalCode',
        as_index=False).agg(lambda x: ', '.join(sorted(set(x))))

# Assigning borough names to 'Not assigned' neighbourhoods

df_PostalCodes.loc[df_PostalCodes['Neighbourhood'] == 'Not assigned',
                   'Neighbourhood'] = df_PostalCodes['Borough']
df_PostalCodes.head(5)
Out[3]:
PostalCode Borough Neighbourhood
0 M1B Scarborough Malvern, Rouge
1 M1C Scarborough Highland Creek, Port Union, Rouge Hill
2 M1E Scarborough Guildwood, Morningside, West Hill
3 M1G Scarborough Woburn
4 M1H Scarborough Cedarbrae
In [56]:
print('Shape:', df_PostalCodes.shape)

Shape: (103, 3)

The extracted data contains numerous issues that were fixed. The neighbourhood data contained postal codes without any boroughs assigned which were dropped. Some neighbourhoods were not assigned a neighbourhood name, so their borough names were assigned to them. In some cases, more than one neighbourhood shared the same postal code. After fixing these issues, the data contained 103 records of postal code data.

In [22]:
# Extracting coordinates data from MapQuest API

df_MQ_Coordinates = pd.DataFrame(columns=['Latitude', 'Longitude'])
for i in range(df_PostalCodes.shape[0]):
    g = geocoder.mapquest(df_PostalCodes.loc[i, 'PostalCode']
                          + ', Toronto, Ontario', key=MapQuest_key)
    df_MQ_Coordinates.loc[i] = g.latlng

Plotting a map of neighbourhoods with MapQuest data

In [4]:
address = 'Toronto, Ontario'
geolocator = Nominatim(user_agent='my-application')
location = geolocator.geocode(address)
latitude = location.latitude
longitude = location.longitude
print('The geograpical coordinates of Toronto, Ontario are {}, {}.'.format(latitude,
        longitude))

The geograpical coordinates of Toronto, Ontario are 43.653963, -79.387207.
In [24]:
df_MQ_Location = pd.concat([df_PostalCodes, df_MQ_Coordinates], axis=1)
map_Toronto_MapQuest = folium.Map(location=[latitude + 0.07,
                                  longitude], zoom_start=11)  # Offset to centre the map around neighbourhoods

# add markers to the map

for (lat, lon, pc, nbh) in zip(df_MQ_Location['Latitude'],
                               df_MQ_Location['Longitude'],
                               df_MQ_Location['PostalCode'],
                               df_MQ_Location['Neighbourhood']):
    label = folium.Popup('{}: {}'.format(pc, nbh), parse_html=True)

    folium.CircleMarker(
        [lat, lon],
        radius=5,
        popup=label,
        color='blue',
        fill=True,
        fill_color='#3186cc',
        fill_opacity=0.7,
        parse_html=False,
        ).add_to(map_Toronto_MapQuest)
map_Toronto_MapQuest
Out[24]:

Fig 01. Toronto neighbourhood map using MapQuest API coordinates

The geographical coordinates data extracted from MapQuest had some concerns too. The postal code data is merged with the coordinates and plotted on a map to get a basic understanding of the data. Following image displays a map of Toronto with neighbourhood markers overlayed on it. It was observed that the MapQuest latitude and longitude were not accurate and many of the nearby neighbourhoods had the same coordinates.

So the coordinates data is replaced by the data extracted from the alternate source, a static CSV file of Google API output. The following image displays a map of Toronto with the neighbourhoods as markers. The latitude of the map is offset by 0.07 to centre the map around the neighbourhoods.

Plotting a map of neighbourhoods with the CSV data from Google API

In [5]:
df_csv_Coordinates = pd.read_csv('http://link.datascience.eu.org/p001d1')
df_csv_Coordinates.rename(columns={'Postal Code': 'PostalCode'},
                          inplace=True)
df_csv_Location = pd.merge(df_PostalCodes, df_csv_Coordinates,
                           on='PostalCode')
In [8]:
map_Toronto_CSV = folium.Map(location=[latitude + 0.07, longitude],
                             zoom_start=11)

# add markers to the map

for (lat, lon, pc, nbh) in zip(df_csv_Location['Latitude'],
                               df_csv_Location['Longitude'],
                               df_csv_Location['PostalCode'],
                               df_csv_Location['Neighbourhood']):
    label = folium.Popup('{}: {}'.format(pc, nbh), parse_html=True)

    folium.CircleMarker(
        [lat, lon],
        radius=5,
        popup=label,
        color='blue',
        fill=True,
        fill_color='#3186cc',
        fill_opacity=0.7,
        parse_html=False,
        ).add_to(map_Toronto_CSV)
map_Toronto_CSV
Out[8]:

Fig 02. Toronto neighbourhood map using Google API coordinates

Examining the maps above, it is evident that the coordinates data from Google API is of better quality than that of MapQuest. Hence, the MapQuest data is discarded and Google coordinates data is used.

In [58]:
df_Location = df_csv_Location.drop(['Borough'], axis=1)
df_Location.head()
Out[58]:
PostalCode Neighbourhood Latitude Longitude
0 M1B Malvern, Rouge 43.806686 -79.194353
1 M1C Highland Creek, Port Union, Rouge Hill 43.784535 -79.160497
2 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711
3 M1G Woburn 43.770992 -79.216917
4 M1H Cedarbrae 43.773136 -79.239476

FourSquare Restaurant data

In [59]:
df_RestaurantTypes = pd.DataFrame(columns=['RestaurantType',
                                  'PostalCode'])
for (index, row) in df_Location.iterrows():
    limit = 100  # limit of number of venues returned by Foursquare API
    radius = 300  # define radius
    cat_id = '4d4b7105d754a06374d81259'  # Category: Food
    url = \
        'https://api.foursquare.com/v2/venues/search?&client_id={}&client_secret={}&v={}&ll={},{}&radius={}&limit={}&categoryId={}'.format(
        FourSquare_client_ID,
        FourSquare_client_secret,
        FourSquare_API_version,
        row['Latitude'],
        row['Longitude'],
        radius,
        limit,
        cat_id,
        )
    df_results = pd.DataFrame(list(venue['categories'][0]['name']
                              for venue in
                              requests.get(url).json()['response'
                              ]['venues']), columns=['RestaurantType'])
    if df_results.shape[0] == 0:
        df_results.loc[0, ['RestaurantType']] = 'No Restaurants'
    df_results['PostalCode'] = row['PostalCode']
    df_RestaurantTypes = pd.concat([df_RestaurantTypes, df_results])
df_RestaurantTypes.reset_index(drop=True, inplace=True)
In [60]:
# Checking FourSquare data

print('Shape:', df_RestaurantTypes.shape)
df_RestaurantTypes.head()

Shape: (1567, 2)
Out[60]:
RestaurantType PostalCode
0 No Restaurants M1B
1 No Restaurants M1C
2 Restaurant M1E
3 Bakery M1E
4 Chinese Restaurant M1E

The FourSquare API returned 1564 records of variables RestaurantType and PostalCode, of which, some locations did not have any restaurants within the specified radius. The RestaurantType variable for such locations was marked as No Restaurants.

Feature Extraction

In [61]:
df_Data = pd.merge(df_Location, df_RestaurantTypes, on='PostalCode')
df_Data.head()
Out[61]:
PostalCode Neighbourhood Latitude Longitude RestaurantType
0 M1B Malvern, Rouge 43.806686 -79.194353 No Restaurants
1 M1C Highland Creek, Port Union, Rouge Hill 43.784535 -79.160497 No Restaurants
2 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 Restaurant
3 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 Bakery
4 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 Chinese Restaurant

Along with the extracted features such as PostalCode, Neighbourhood, Latitude, Longitude and RestaurantType, a new variable for the distance of the location from the city centre is added as Distance.

The Distance of a location x1 from the city centre x is calculated using the famous Pythagoras theorem. However, latitudes and longitudes do not follow the same scale throughout the globe. The distance between any two consecutive latitudes is 111 kilometres, but the distance between two consecutive longitudes varies depending on where on Earth we are measuring it. The distance between two longitudes at the Equator is 111 kilometres but it gradually decreases as we move away from the Equator and toward the poles. The information at the National Oceanic and Atmospheric Administration website is used to calculate the approximate distance between two consecutive longitudes in Toronto to be 80 kilometres. The following image illustrates the calculation of the distance of a location from Toronto city centre.

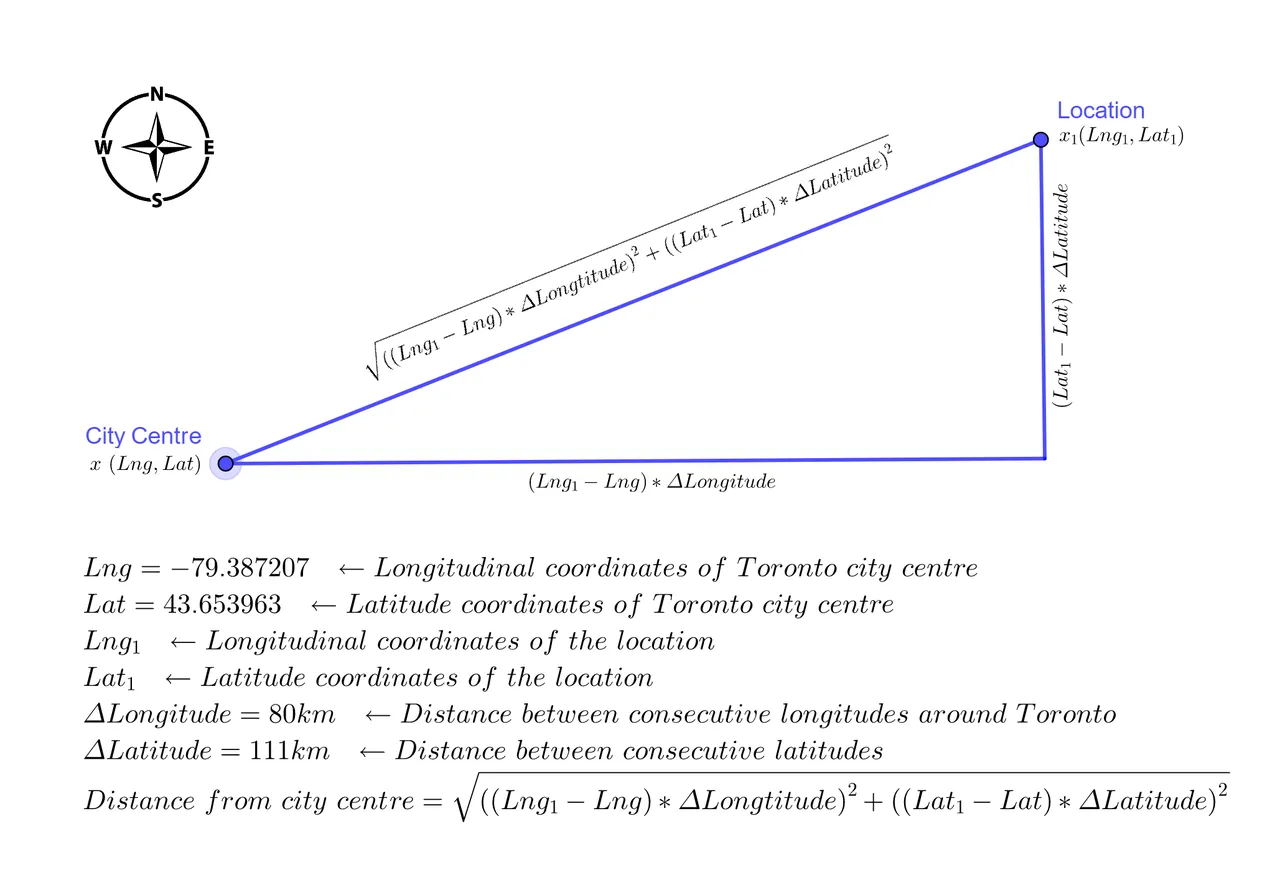
Fig 03. Distance of a location from city centre using Pythagoras theorem

In [62]:
# Distance between two consecutive longitudes in Toronto in kilometers
dLng = 80
# Distance between two consecutive latitudes in kilometers
dLat = 111
df_Data.insert(4, 'Distance', (((df_Data['Longitude'] - longitude)
               * dLng) ** 2 + ((df_Data['Latitude'] - latitude) * dLat)
               ** 2) ** 0.5)
df_Data.head()
Out[62]:
PostalCode Neighbourhood Latitude Longitude Distance RestaurantType
0 M1B Malvern, Rouge 43.806686 -79.194353 22.921869 No Restaurants
1 M1C Highland Creek, Port Union, Rouge Hill 43.784535 -79.160497 23.216478 No Restaurants
2 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 Restaurant
3 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 Bakery
4 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 Chinese Restaurant

Following are the extracted and calculated features of the data frame df_Data used in the analysis.

Feature Source Description Purpose
PostalCode Extracted from Wikipedia A three-letter alphanumeric postcode of a neighbourhood in Toronto Primary key to merge various data frames.
Neighbourhood Extracted from Wikipedia One or more neighbourhood names that fall within the area of the postcode. A key variable around which the analysis is done. Also used as markers on the map.
Latitude Extracted from MapQuest or Google API Latitude of the postcode in decimal units. To locate neighbourhoods on the map and to calculate the distance of a location from the city centre.
Longitude Extracted from MapQuest or Google API Longitude of the postcode in decimal units. To locate neighbourhoods on the map and to calculate the distance of a location from the city centre.
Distance Calculated Distance of a location from the city centre in kilometres. To calculate the correlation between the distance of a location from the city centre and the number of restaurants in the location.
RestaurantType Extracted from FourSquare API Type of a restaurant. To partition the city of Toronto into various clusters based on restaurant types located in the city. Also used to find possible correlations between various restaurant types within the city.
In [82]:
# Run this code if you are not using FourSquare API
# A copy of df_Data data frame is available for download
# from https://link.datascience.eu.org/p001d2

df_Data = pd.read_csv('http://link.datascience.eu.org/p001d2', encoding='utf-8')
df_Data.head()
Out[82]:
PostalCode Neighbourhood Latitude Longitude Distance RestaurantType
0 M1B Malvern, Rouge 43.806686 -79.194353 22.921869 No Restaurants
1 M1C Highland Creek, Port Union, Rouge Hill 43.784535 -79.160497 23.216478 No Restaurants
2 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 Bakery
3 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 Restaurant
4 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 Chinese Restaurant

Exploratory Data Analysis - Clustering Toronto neighbourhoods by restaurant types

K-Means Clustering

Clustering or cluster analysis is the process of dividing data into groups (clusters) in such a way that objects in the same cluster are more similar to each other than those in other clusters. The goal is to divide Toronto neighbourhoods into various groups based on the top 10 types of restaurants located in the neighbourhoods. There are various models and techniques for cluster analysis. K-means clustering is a simple unsupervised learning algorithm that is commonly used for market segmentation. The RestaurantType column is first one-hot encoded and grouped by PostalCode.

One-hot encoding and grouping by postal codes

In [72]:
df_Clusters = df_Data.copy()

# df_OneHot = pd.get_dummies(df_Clusters[["RestaurantType"]], prefix="", prefix_sep="", drop_first=True)

df_Clusters = df_Clusters.drop('RestaurantType',
                               axis=1).join(pd.get_dummies(df_Clusters[['RestaurantType'
        ]], prefix='', prefix_sep=''))
print(df_Clusters.shape)
df_Clusters.head(5)

(1564, 125)
Out[72]:
PostalCode Neighbourhood Latitude Longitude Distance ... Turkish Restaurant Vegetarian / Vegan Restaurant Vietnamese Restaurant Wine Bar Wings Joint
0 M1B Malvern, Rouge 43.806686 -79.194353 22.921869 ... 0 0 0 0 0
1 M1C Highland Creek, Port Union, Rouge Hill 43.784535 -79.160497 23.216478 ... 0 0 0 0 0
2 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 ... 0 0 0 0 0
3 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 ... 0 0 0 0 0
4 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 ... 0 0 0 0 0

5 rows × 125 columns

In [73]:
df_Clusters = df_Clusters.groupby(['PostalCode', 'Neighbourhood',
                                  'Latitude', 'Longitude', 'Distance'
                                  ]).sum().reset_index()
print(df_Clusters.shape)
df_Clusters.head()

(103, 125)
Out[73]:
PostalCode Neighbourhood Latitude Longitude Distance ... Turkish Restaurant Vegetarian / Vegan Restaurant Vietnamese Restaurant Wine Bar Wings Joint
0 M1B Malvern, Rouge 43.806686 -79.194353 22.921869 ... 0 0 0 0 0
1 M1C Highland Creek, Port Union, Rouge Hill 43.784535 -79.160497 23.216478 ... 0 0 0 0 0
2 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 ... 0 0 0 0 0
3 M1G Woburn 43.770992 -79.216917 18.823836 ... 0 0 0 0 0
4 M1H Cedarbrae 43.773136 -79.239476 17.738704 ... 0 0 0 0 0

5 rows × 125 columns

Following are the top 10 types of restaurants in Toronto

In [74]:
top_count = 10  # Number of top restaurant types
top_restaurant_types = df_Clusters[list(df_Clusters.iloc[:, 5:
                                   ])].sum(axis=0).reset_index().sort_values(by=0,
        ascending=False).iloc[:top_count]['index'].values.tolist()
print(tabulate(pd.DataFrame({'Top 10 restaurant types': top_restaurant_types}).set_index('Top 10 restaurant types'
               ), headers='keys', tablefmt='psql'))

+---------------------------+
| Top 10 restaurant types   |
|---------------------------|
| Coffee Shop               |
| Café                      |
| Restaurant                |
| Pizza Place               |
| Fast Food Restaurant      |
| Italian Restaurant        |
| Sandwich Place            |
| Bakery                    |
| Sushi Restaurant          |
| Breakfast Spot            |
+---------------------------+

Determining the optimal k

In [75]:
# Determining optimal k

df_kmeans = df_Clusters[top_restaurant_types]
distortions = []
K = range(1, 10)
for k in K:
    kmeans = KMeans(n_clusters=k, random_state=3).fit(df_kmeans)
    distortions.append(kmeans.inertia_)
plt.plot(K, distortions, 'bx-')
plt.xlabel('k')
plt.ylabel('Distortion')
plt.title('Fig 04. The Elbow method showing the optimal k')
plt.show()
No description has been provided for this image

The optimal value of the number of clusters, k, is determined using the elbow method to be 3.

In [76]:
k = 3  # Number of clusters
kmeans = KMeans(n_clusters=k, random_state=3).fit(df_kmeans)
# df_Clusters.insert(2, 'Cluster', kmeans.labels_)
df_Clusters['Cluster']=kmeans.labels_
df_Clusters.head(5)
Out[76]:
PostalCode Neighbourhood Latitude Longitude Distance ... Vegetarian / Vegan Restaurant Vietnamese Restaurant Wine Bar Wings Joint Cluster
0 M1B Malvern, Rouge 43.806686 -79.194353 22.921869 ... 0 0 0 0 0
1 M1C Highland Creek, Port Union, Rouge Hill 43.784535 -79.160497 23.216478 ... 0 0 0 0 0
2 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 ... 0 0 0 0 0
3 M1G Woburn 43.770992 -79.216917 18.823836 ... 0 0 0 0 0
4 M1H Cedarbrae 43.773136 -79.239476 17.738704 ... 0 0 0 0 0

5 rows × 126 columns

The neighbourhoods are grouped into three clusters. The following table shows the cluster number and the number of neighbourhoods in each cluster.

In [77]:
# Pretty-printing clusters in tabular format.

print(tabulate(df_Clusters['Cluster'
               ].value_counts().sort_index().to_frame(),
               headers=['Cluster number',
               'Neighbourhoods in the cluster'], tablefmt='psql',
               colalign=('center', 'center')))

+------------------+---------------------------------+
|  Cluster number  |  Neighbourhoods in the cluster  |
|------------------+---------------------------------|
|        0         |               79                |
|        1         |               13                |
|        2         |               11                |
+------------------+---------------------------------+
In [79]:
# This code is optional
# A copy of df_Clusters is available for download
# at https://link.datascience.eu.org/p001d3

df_Clusters = pd.read_csv('http://link.datascience.eu.org/p001d3', encoding='utf-8')
df_Clusters.head()
Out[79]:
PostalCode Neighbourhood Latitude Longitude Distance ... Vegetarian / Vegan Restaurant Vietnamese Restaurant Wine Bar Wings Joint Cluster
0 M1B Malvern, Rouge 43.806686 -79.194353 22.921869 ... 0 0 0 0 0
1 M1C Highland Creek, Port Union, Rouge Hill 43.784535 -79.160497 23.216478 ... 0 0 0 0 0
2 M1E Guildwood, Morningside, West Hill 43.763573 -79.188711 20.004767 ... 0 0 0 0 0
3 M1G Woburn 43.770992 -79.216917 18.823836 ... 0 0 0 0 0
4 M1H Cedarbrae 43.773136 -79.239476 17.738704 ... 0 0 0 0 0

5 rows × 126 columns

Visualization

The image is a visualization of neighbourhood clusters displayed on a map of Toronto. Each cluster is marked by a different colour to easily distinguish it from other clusters. The map enables viewers to visualize the locations of the city fall into various segregations based on their types of restaurants.

In [83]:
# create map

map_clusters = folium.Map(location=[latitude + 0.07, longitude],
                          tiles='OpenStreetMap', zoom_start=11)

# set color scheme for the clusters

colours = ['green', 'blue', 'red']

# add markers to the map

markers_colors = []
for (lat, lng, pc, nbh, cluster) in zip(df_Clusters['Latitude'],
        df_Clusters['Longitude'], df_Clusters['PostalCode'],
        df_Clusters['Neighbourhood'], df_Clusters['Cluster']):
    label = folium.Popup(str(pc) + ': ' + str(nbh) + ' Cluster '
                         + str(cluster), parse_html=True)

    folium.CircleMarker(
        [lat, lng],
        radius=5,
        popup=label,
        color=colours[cluster],
        fill=True,
        fill_color=colours[cluster],
        fill_opacity=0.6,
        ).add_to(map_clusters)
map_clusters
Out[83]:

Fig 05. Map of Toronto clustered by restaurant types

Market insights

Examining each cluster individually and then by comparing it with other clusters provides valuables insights into Toronto's foodservice market.

In [84]:
for colour in sorted(colours, reverse=True):
    df = df_Clusters.loc[df_Clusters['Cluster']
                         == colours.index(colour)].copy()
    df.drop([
        'PostalCode',
        'Neighbourhood',
        'Latitude',
        'Longitude',
        'Distance',
        'Cluster',
        ], axis=1, inplace=True)
    Rcount = df.sum().sum()
    Ncount = df.shape[0]
    N0count = df['No Restaurants'].sum()
    RperN = int(round(Rcount / (Ncount - N0count)))
    N0percentage = int(round(N0count * 100 / Ncount))
    print('''Cluster: {}
Restaurants in the cluster: {}
Neighbourhoods in the cluster: {}
Percentage of neighbourhoods without restaurants: {}%
Restaurants per neighbourhood: {}'''.format(colour.title(),
            Rcount, Ncount, N0percentage, RperN))
    print(tabulate(df.sum().sort_values(ascending=False).head().to_frame(),
           headers=['Top restaurant types in the cluster', 'Count'
           ], tablefmt='psql'), '\n')

Cluster: Red
Restaurants in the cluster: 549
Neighbourhoods in the cluster: 11
Percentage of neighbourhoods without restaurants: 0%
Restaurants per neighbourhood: 50
+---------------------------------------+---------+
| Top restaurant types in the cluster   |   Count |
|---------------------------------------+---------|
| Coffee Shop                           |     125 |
| Restaurant                            |      38 |
| Café                                  |      23 |
| Food Court                            |      20 |
| Fast Food Restaurant                  |      19 |
+---------------------------------------+---------+ 

Cluster: Green
Restaurants in the cluster: 443
Neighbourhoods in the cluster: 79
Percentage of neighbourhoods without restaurants: 25%
Restaurants per neighbourhood: 8
+---------------------------------------+---------+
| Top restaurant types in the cluster   |   Count |
|---------------------------------------+---------|
| Coffee Shop                           |      39 |
| Café                                  |      34 |
| Fast Food Restaurant                  |      21 |
| No Restaurants                        |      20 |
| Pizza Place                           |      20 |
+---------------------------------------+---------+ 

Cluster: Blue
Restaurants in the cluster: 572
Neighbourhoods in the cluster: 13
Percentage of neighbourhoods without restaurants: 0%
Restaurants per neighbourhood: 44
+---------------------------------------+---------+
| Top restaurant types in the cluster   |   Count |
|---------------------------------------+---------|
| Coffee Shop                           |      61 |
| Pizza Place                           |      41 |
| Café                                  |      37 |
| Italian Restaurant                    |      26 |
| Restaurant                            |      26 |
+---------------------------------------+---------+

The red cluster has 11 neighbourhoods that are located closest to the city centre. With 50 restaurants per neighbourhood, it has the highest density of restaurants in the city. Besides having the highest number of coffee shops, it also has a high number of restaurants followed by food courts and fast food centres. It is also interesting to note that all neighbourhoods in this group have restaurants. This cluster is a thriving market for foodservice industry but start-ups may also face stiff competition.

The green cluster consists of 79 neighbourhoods. This group has the lowest concentration of 8 restaurants per neighbourhood. It's top food services are coffee shops, café, fast food restaurants and pizza places. The number of restaurants of each type is more or less proportional, unlike the red cluster where the coffee shops were about three times more than any other restaurant type. It is important to note that 25% of these neighbourhoods have no restaurants at all. This is a great opportunity for new start-ups to perform further market research. This cluster is also spread out uniformly throughout the city. With moderate competition and a variety of restaurant types, the neighbourhoods in this cluster might be a good choice to start up a new restaurant, especially if it is from the top restaurant categories of this cluster.

The blue cluster consists of 13 neighbourhoods with a high average concentration of 44 restaurants per neighbourhood. All neighbourhoods have restaurants. This cluster has the most proportionally distributed types of restaurants of all. Though coffee shops dominate the market, there are a good number of pizza places, cafés, Italian and other restaurants. These neighbourhoods are possibly one of the promising locations to start a new pizza place or an Italian restaurant.

Inferential Data Analysis

In [85]:
df_correlation = df_Clusters.drop(['PostalCode', 'Neighbourhood',
                                  'Cluster', 'Latitude', 'Longitude'],
                                  axis=1)
df_correlation.head()
Out[85]:
Distance Afghan Restaurant African Restaurant American Restaurant Argentinian Restaurant ... Turkish Restaurant Vegetarian / Vegan Restaurant Vietnamese Restaurant Wine Bar Wings Joint
0 22.921869 0 0 0 0 ... 0 0 0 0 0
1 23.216478 0 0 0 0 ... 0 0 0 0 0
2 20.004767 0 0 0 0 ... 0 0 0 0 0
3 18.823836 0 0 0 0 ... 0 0 0 0 0
4 17.738704 0 0 0 0 ... 0 0 0 0 0

5 rows × 121 columns

The following image illustrates any possible correlations between data variables.

In [86]:
corr = df_correlation.corr()
(fig, ax) = plt.subplots(figsize=(18, 18))
sns.heatmap(
    corr,
    xticklabels=corr.columns.values,
    yticklabels=corr.columns.values,
    ax=ax,
    cmap='RdBu',
    vmin=-1,
    vmax=1,
    )
plt.title('Fig 06. Correlation heatmap', fontsize=18)
plt.show()
No description has been provided for this image

Key observations:

  • The red markers indicate the possibility of a negative correlation between Distance and number of restaurants.
  • Possible positive correlations between a few restaurant types

Relationship between the location of the neighbourhood and the number of restaurants in it.

In [87]:
df_Distance = df_correlation[['Distance']].copy()
df_Distance['RestaurantCount'] = df_correlation.drop(['Distance',
        'No Restaurants'], axis=1).sum(axis=1)
df_Distance.head()
Out[87]:
Distance RestaurantCount
0 22.921869 0
1 23.216478 0
2 20.004767 4
3 18.823836 1
4 17.738704 8
In [88]:
# Correlation coefficient(r) and p-value

(r, p) = pearsonr(df_Distance['Distance'], df_Distance['RestaurantCount'])
print('Correlation coefficient: {}, p_value: {}'.format(r, p))

Correlation coefficient: -0.6292700966010896, p_value: 1.0882133680915895e-12

A correlation coefficient of -0.63 indicates a moderately strong negative correlation between the distance of a neighbourhood from the city centre and the number of restaurants located in the neighbourhood. A negligible p-value of 1.09e-12 implies the correlation is statistically significant. The following chart graphically represents the relationship between the two variables. This implies that foodservice market in Toronto is highly concentrated around the city centre and becomes sparser as we move farther. It can be speculated that the restaurant market is driven by large demand and strong competition at the centre of the city and their demand dampens toward the city limits, however, additional research is required to reach to such conclusions.

In [89]:
plt.subplots(figsize=(15, 10))
sns.regplot(x=df_Distance['Distance'], y=df_Distance['RestaurantCount'
            ]).set_title('Fig 07. Correlation between distance and number of restaurants. r={}, p={:.2e}'.format(round(r,
                         4), p), fontsize=16)
plt.ylim(0, None)
plt.ylabel('Number of restaurants in the neighbourhood', fontsize=14)
plt.xlabel('Distance of the neighbourhood from city centre', fontsize=14)
plt.show()
No description has been provided for this image

Relationships between types of restaurants

Correlations

In [90]:
# Data frame of restaurant types
df_correlation = df_Clusters.drop(["PostalCode","Neighbourhood","Distance","Cluster","Latitude","Longitude"],axis=1)
df_correlation.head()
Out[90]:
Afghan Restaurant African Restaurant American Restaurant Argentinian Restaurant Asian Restaurant ... Turkish Restaurant Vegetarian / Vegan Restaurant Vietnamese Restaurant Wine Bar Wings Joint
0 0 0 0 0 0 ... 0 0 0 0 0
1 0 0 0 0 0 ... 0 0 0 0 0
2 0 0 0 0 0 ... 0 0 0 0 0
3 0 0 0 0 0 ... 0 0 0 0 0
4 0 0 0 0 0 ... 0 0 0 0 0

5 rows × 120 columns

As observed in the correlation heatmap earlier (in Fig 06), there was some positive correlation in blue among most restaurant types. Since we are interested in moderate to strong correlations, we can ignore restaurants with mild or no correlations to reduce the clutter. Following is a visualization of restaurant types with correlation coefficients greater than 0.7.

In [91]:
# Correlation between restaurant types
correlation = df_correlation.corr()
correlation = correlation.mask((correlation > -0.7) & (correlation
                               < 0.7), 0)
(fig, ax) = plt.subplots(figsize=(18, 18))
sns.heatmap(
    correlation,
    xticklabels=correlation.columns.values,
    yticklabels=correlation.columns.values,
    ax=ax,
    cmap='RdBu',
    vmin=-1,
    vmax=1,
    )
plt.title('Fig 08. Correlation heatmap of types of restaurants', fontsize=18)
plt.show()
No description has been provided for this image

Also, some restaurant pairs hold strong correlations but the number of such restaurants is so small that their correlations are practically insignificant. In this case, we are interested in correlations between restaurants that have at least five restaurants of their type in the city. Any restaurant type with less than 5 restaurants is dropped from further analysis.

Regression coefficients (Pearson r) and p-values are calculated from Pearsons regression. Only coefficients greater than 0.7 are considered. For a 99% confidence study, we take in to account only the restaurant pairs with p less than an $\alpha$ of 0.01.

Following is the list of features and correlation heatmap of restaurant types r > 0.7 and p < 0.01.

In [92]:
# Adding a totals row containing the number of restaurants of each type.

df_correlation.loc['Total'] = df_correlation.sum()
df_correlation.loc['Total']
Out[92]:
Afghan Restaurant                 1
African Restaurant                2
American Restaurant              25
Argentinian Restaurant            1
Asian Restaurant                 17
                                 ..
Turkish Restaurant                2
Vegetarian / Vegan Restaurant    21
Vietnamese Restaurant            10
Wine Bar                          1
Wings Joint                       9
Name: Total, Length: 120, dtype: int64
In [93]:
# Dropping restaurants types that have less than five restaurants in the city.

print('All restaurant types:', df_correlation.shape[1])
for col in df_correlation.columns:
    if df_correlation.loc['Total', col] < 5:
        df_correlation.drop(col, axis=1, inplace=True)
df_correlation.drop('Total', axis=0, inplace=True)
print('Restaurant types with at least 5 restaurants:', df_correlation.shape[1])

All restaurant types: 120
Restaurant types with at least 5 restaurants: 61
In [94]:
def compute_correlation(df):
    df = df.dropna()._get_numeric_data()
    dfcols = pd.DataFrame(columns=df.columns)
    rmatrix = dfcols.transpose().join(dfcols, how='outer')
    featureList = []
    count = 0
    for row in df.columns:
        for col in df.columns[count:]:
            (r, p) = pearsonr(df[row], df[col])
            if abs(r - 1) > 0.01 and r > 0.7 and p < 0.01:
                featureList.append([row, col, r, p])
                rmatrix[row][col] = r
                rmatrix[col][row] = r
        count += 1
    rmatrix.fillna(value=np.nan, inplace=True)
    df_Features = pd.DataFrame(sorted(featureList, reverse=True,
                               key=lambda x: x[2]),
                               columns=['Restaurant Type 1',
                               'Restaurant Type 2',
                               "Correlation Coefficient 'r'", 'p-value'
                               ])
    return (rmatrix, df_Features)
In [95]:
(rmatrix, df_Features) = compute_correlation(df_correlation)
df_Features.shape[0]
Out[95]:
8

Following is the list of restaurants with significant positive correlations.

In [96]:
print(tabulate(df_Features, headers='keys', tablefmt='psql',
               colalign=('left', 'left', 'left', 'center', 'center')))

+----+---------------------+---------------------+-------------------------------+-------------+
|    | Restaurant Type 1   | Restaurant Type 2   |  Correlation Coefficient 'r'  |   p-value   |
|----+---------------------+---------------------+-------------------------------+-------------|
| 0  | Deli / Bodega       | Food Court          |           0.809164            | 4.61791e-25 |
| 1  | Coffee Shop         | Restaurant          |           0.774627            | 8.09654e-22 |
| 2  | Italian Restaurant  | Thai Restaurant     |           0.765077            | 5.07373e-21 |
| 3  | Salad Place         | Sports Bar          |           0.741198            | 3.49179e-19 |
| 4  | Bar                 | Deli / Bodega       |            0.73927            | 4.81547e-19 |
| 5  | Bubble Tea Shop     | Ramen Restaurant    |           0.730993            | 1.85416e-18 |
| 6  | Convenience Store   | Food Court          |           0.721358            | 8.37724e-18 |
| 7  | Coffee Shop         | Japanese Restaurant |           0.716494            | 1.75161e-17 |
+----+---------------------+---------------------+-------------------------------+-------------+
In [97]:
for col in rmatrix:
    if rmatrix[col].sum() == 0:
        rmatrix.drop(col, axis=1, inplace=True)
        rmatrix.drop(col, axis=0, inplace=True)
rmatrix
Out[97]:
Bar Bubble Tea Shop Coffee Shop Convenience Store Deli / Bodega ... Ramen Restaurant Restaurant Salad Place Sports Bar Thai Restaurant
Bar NaN NaN NaN NaN 0.73927 ... NaN NaN NaN NaN NaN
Bubble Tea Shop NaN NaN NaN NaN NaN ... 0.730993 NaN NaN NaN NaN
Coffee Shop NaN NaN NaN NaN NaN ... NaN 0.774627 NaN NaN NaN
Convenience Store NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN
Deli / Bodega 0.73927 NaN NaN NaN NaN ... NaN NaN NaN NaN NaN
... ... ... ... ... ... ... ... ... ... ... ...
Ramen Restaurant NaN 0.730993 NaN NaN NaN ... NaN NaN NaN NaN NaN
Restaurant NaN NaN 0.774627 NaN NaN ... NaN NaN NaN NaN NaN
Salad Place NaN NaN NaN NaN NaN ... NaN NaN NaN 0.741198 NaN
Sports Bar NaN NaN NaN NaN NaN ... NaN NaN 0.741198 NaN NaN
Thai Restaurant NaN NaN NaN NaN NaN ... NaN NaN NaN NaN NaN

13 rows × 13 columns

In [98]:
ax = plt.subplots(figsize=(16, 12))[1]
mask = np.zeros_like(rmatrix)
mask[np.triu_indices_from(mask)] = True
sns.heatmap(
    rmatrix,
    xticklabels=rmatrix.columns.values,
    yticklabels=rmatrix.columns.values,
    mask=mask,
    ax=ax,
    cmap='RdBu',
    vmin=-1,
    vmax=1,
    annot=True,
    square=True,
    )
plt.title('Fig 09. Correlation heatmap displaying Pearson coefficients', fontsize=16)
plt.xlabel('Restaurant types', fontsize=12)
plt.ylabel('Restaurant types', fontsize=12)
plt.show()
No description has been provided for this image

Regression Analysis

In [99]:
count = df_Features.shape[0]
cols = 4 # Number of columns of plots
scale = 4 # Plot size scale
rows = int(count / cols)
if rows * cols < count:
    rows += 1
rtxt = "Correlation Coefficient 'r'"
ptxt = 'p-value'
(fig, axs) = plt.subplots(nrows=rows, ncols=cols, figsize=(int(cols * scale),
                          int(rows * scale)))
for (i, ax) in zip(range(count), axs.flat):
    sns.regplot(x=df_correlation[df_Features['Restaurant Type 1'][i]],
                y=df_correlation[df_Features['Restaurant Type 2'][i]],
                ax=ax)
    ax.text(
        0.5,
        0.95,
        '{} = {:.4f}'.format(rtxt, df_Features[rtxt][i]),
        fontsize=8,
        ha='center',
        va='center',
        transform=ax.transAxes,
        )
    ax.text(
        0.5,
        0.90,
        '{} = {:.2e}'.format(ptxt, df_Features[ptxt][i]),
        fontsize=8,
        ha='center',
        va='center',
        transform=ax.transAxes,
        )
fig.suptitle('Fig 10: Top {} correlation and regression charts'.format(count), fontsize=16)
fig.tight_layout()
fig.subplots_adjust(top=0.9, hspace=0.3, wspace=0.25)
plt.show()
No description has been provided for this image

The above figure illustrates eight pairs of restaurant types with a strong positive correlation between each other. All the pairs have p-values much lesser than an $\alpha$ of 0.01 indicating high statistical significance. For example, in chart 1, neighbourhoods with a high number of Food Court restaurants also have a relatively high number of Deli / Bodega restaurants. So if someone plans to open a deli in Toronto, it may be a good idea to choose a location with a good number of food courts. Similarly, in chart 2, it may be profitable to open a coffee shop in a location with restaurants. Similar inferences can be made with all the pairs of restaurants from the charts above.

Conclusions

In this study, cluster analysis and correlation/regression analysis are used to explore valuable insights into Toronto foodservice market. The city is divided into several clusters based on types of restaurants to give a bird's eye view of market trends. The inverse relationship between the number of restaurants in a location and the distance of the location from the city centre indicate that the restaurant industry flourishes when it's closer to the centre. Strong positive correlations between pairs of restaurants help investors to decide better on profitable locations for their new ventures

Future directions

The study analyzes the restaurant market based on the number of restaurants in the location. The analysis can be greatly enhanced by taking profitability into account. This project could be further improved by adding factors such as demand, competition, population, etc into consideration.

Download/view project report: [PDF]

References

[1] “Foodservice Industry Forecast 2018-2022,” Restaurants Canada (formerly CRFA). https://www.restaurantscanada.org/resources/foodservice-industry-forecast/

[2] “The Canadian Restaurant Industry Landscape – why is Toronto Unique?” CHD Expert. https://www.chd-expert.com/blog/press_release/the-canadian-restaurant-industry-landscape-why-is-toronto-unique/

[3] “Pythagorean theorem,” Wikipedia. https://en.wikipedia.org/wiki/Pythagorean_theorem

[4] “Latitude/Longitude Distance Calculator,” National Oceanic and Atmospheric Administration - National Hurricane Center and Central Pacific Hurricane Center. https://www.nhc.noaa.gov/gccalc.shtml

[5] “Determining the number of clusters in a data set,” Wikipedia. https://en.wikipedia.org/wiki/Determining_the_number_of_clusters_in_a_data_set#The_elbow_method

[6] “Pearson Correlation and Linear Regression,” University of Texas - Austin. http://sites.utexas.edu/sos/guided/inferential/numeric/bivariate/cor/

[7] “Simple Linear Regression and Correlation,” StatsDirect Limited. https://www.statsdirect.com/help/regression_and_correlation/simple_linear.htm

Comments